Abstract

We present a new non-dominated sorting algorithm to generate the non-dominated fronts in multi-objective optimization with evolutionary algorithms, particularly the NSGA-II. The non-dominated sorting algorithm used by NSGA-II has a time complexity of O(MN2) in generating non-dominated fronts in one generation (iteration) for a population size N and M objective functions. Since generating non-dominated fronts takes the majority of total computational time (excluding the cost of fitness evaluations) of NSGA-II, making this algorithm faster will significantly improve the overall efficiency of NSGA-II and other genetic algorithms using non-dominated sorting. The new non-dominated sorting algorithm proposed in this study reduces the number of redundant comparisons existing in the algorithm of NSGA-II by recording the dominance information among solutions from their first comparisons. By utilizing a new data structure called the dominance tree and the divide-and-conquer mechanism, the new algorithm is faster than NSGA-II for different numbers of objective functions. Although the number of solution comparisons by the proposed algorithm is close to that of NSGA-II when the number of objectives becomes large, the total computational time shows that the proposed algorithm still has better efficiency because of the adoption of the dominance tree structure and the divide-and-conquer mechanism.

Introduction

Design optimization for many engineering applications is multi-objective in nature. For most multi-objective problems, the objectives conflict with each other, and it is impossible to obtain a single set of values for the design variables that corresponds to the optima of all the objectives. In this situation, an optimal solution represents a certain the optima of all the objectives. In this situation, an optimal solution represents a certain level of trade-offs among all of the objectives, and a set of trade-off solutions exists for a multi-objective optimization problem. The set containing all the trade-off solutions is formally called the Pareto front^[1], and the solutions on the Pareto front are also called non-dominated solutions. Therefore, solving a multi-objective optimization problem refers to obtaining a subset of the solutions on the Pareto front instead of getting each objective’s optimum.

The Non-dominated Sorting Algorithm of NSGA-II

In each generation in NSGA-II, genetic operators are applied to the parent population to obtain an equal sized child population. The parent and child are then combined to form a temporary population on which the non-dominated sorting algorithm is applied to generate the non-dominated fronts. Therefore, the population size for non-dominated sorting is twice as large as the parent population. The population for the next generation has the same size as the parent population; its solutions are selected from non-dominated fronts with the highest ranks. The solutions within a front are sorted by crowding-distances so that those with the largest crowding distances are selected into the next generation, if only a portion of the front can be selected. Details about the definition and sorting algorithm of crowding-distance sorting can be found in the literature. ^[2] Figure 1 illustrates the schematic procedure of NSGA-II in one generation. In NSGA-II, non-dominated fronts are obtained one after another starting from the one with the highest rank to the one with the lowest rank. The procedure for generating the first front of a population of N solutions is as follows.

1. Create a population P by combining the parent and offspring populations.
2. Create an empty front F. Remove the first solution s1 from P and put s1 into F.
3. Compare the second solution s2 in P with s1. If s1 dominates s2, s2 remains in P and go to next step; otherwise, remove s2 from P and put it into F. If s1 is dominated by s2, remove s1 from F and put it back to P; otherwise, s1 and s2 are non-dominated.
4. Compare si (i = 3, 4, . . .,N) in P with all solutions in F. If solution si is dominated by a solution in F, si remains in P. Any solutions in F dominated by si are removed from F and put back into P. If si is not dominated after all the comparisons, si is removed from P and put into F.

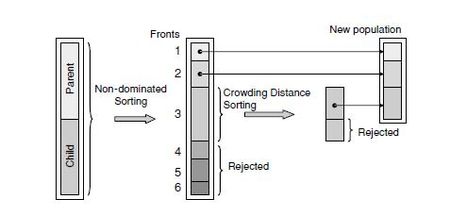
Figure 1: Schematic procedure of NSGA-II

The New Non-dominated Sorting Algorithm

The basic idea of the proposed non-dominated sorting algorithm is that, if the dominance information from the first comparisons can be saved for any two solutions, we can then eliminate the redundant comparisons between the same pairs of solutions. Furthermore, we do not even need to compare all the pairs of solutions. For example, if Solution A is found to dominate Solution B, all solutions already found being dominated by Solution B do not need to compare with Solution A, because they are all dominated by Solution A. Because the dominance information among solutions is hierarchical, a hierarchical data structure, that is, a tree structure, is preferred to save the dominance information. In this study, we used the dominance tree presented in Figure 2 for this purpose. We also adopted the divide-and-conquer mechanism to make the new algorithm faster and more efficient in obtaining the dominance information.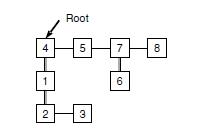

Figure 2: Dominance tree of eight solutions

The Dominance Tree

A data structure was developed called the dominance tree to save the dominance information among solutions in order to reduce the number of repetitive comparisons. The basic unit of a dominance tree is called a node, which keeps a solution and is linked to other nodes. There are two types of links between any two nodes, the non-dominance link and the dominance link. The nodes connected with a non-dominance link are called siblings whose solutions are non-dominated. The nodes connected with a dominance link are called parent and child, respectively, with the solution in the parent node dominating the one in the child node. The dominance tree for the example problem in Section 2 is shown in Figure 3, in which 4, 5, 7, and 8 are sibling nodes and Node 4 (parent) dominates Node 1 (child). If several sibling nodes are dominated by the same parent node, only one dominance link is needed between the parent node and the first sibling node. This is the case for Nodes 1, 2, and 3 in Figure 2.

Figure 3: New Sorting Algorithm

Conclusions

A new non-dominated sorting algorithm has been developed that can be used in evolutionary algorithms, particularly the NSGA-II, to efficiently generate the nondominated fronts. The new algorithm adopts the divide-and-conquer mechanism and uses a new data structure called the dominance tree to achieve both time and space efficiency. The comparisons of the new algorithm with the non-dominated sorting algorithm currently used in NSGA-II showed that the former always performed better for different numbers of objectives and population sizes. Although the reduction on the number of redundant comparisons by the new algorithm becomes less significant when the number of objectives increases, the speedup of the new algorithm on the total processing time is still significant even for a large number of objectives. The nondominated fronts generated by the new algorithm for different numbers of objectives and population sizes were also verified and shown to be identical to those generated by the algorithm of NSGA-II.

Original Paper

This page is a shortened version of the original paper found here

References

1. ↑ Coello, C. A. C. (1999). A comprehensive survey of evolutionary-based multi-objective optimization techniques. Knowledge and Information Systems, 1:269–308
2. ↑ Deb, K., Pratab, A., Agarwal, S., and Meyarivan, T. (2002). A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Comput ation, 6:182–197