Integrated Computational Materials Engineering (ICME)
Uncertainty of a Physically Motivated Internal State Variable Plasticity and Damage Model
Authors: K.N. Solanki, M.F. Horstemeyer, W.G. Steele, Y. Hammi, J.B. Jordon
DOI: https://doi.org/10.1016/j.ijsolstr.2009.09.025
Abstract
Here, we illustrate a formal calibration, validation, and verification process that includes uncertainty in an internal state variable plasticity-damage model that is implemented in a finite element code. The physically motivated continuum model characterizes damage evolution by incorporating material uncertainty due to microstructural spatial clustering. The uncertainty analysis is performed by introducing material variation through model validation and verification. The effect of variability in microstructural clustering and boundary conditions on the sensitivities and uncertainty of the plasticity-damage evolution for the 7075 aluminum alloy is characterized. The results show the potential of this methodology in the evaluation of material response uncertainty due to microstructure spatial clustering and its effect on damage evolution. For damage evolution, we have shown that the initial isotropic damage evolved into an anisotropic form as the deformation increased which is consistent with experimentally observed behavior for 7075 aluminum alloy in literature. Also, the sensitivities were found to be consistent with the physics of damage progression for this particular type of material. Through the sensitivity analysis, the initial defect size and number density of cracked particles are important at the beginning of deformation. As damage evolves, more voids are nucleated and grow and the sensitivity analysis illustrates this as well. Then, voids combine with each other and coalescence becomes the main driver, which is also confirmed by the sensitivity analysis. This work also shows that the microstructurally-based damage evolution equations provide an accurate representation of the damage progression due to large intermetallic particles. Finally, we illustrate that the initial variation in the microstructure clustering can lead to about ±7.0%, ±8.1%, and ±9.75% variation in the elongation to failure strain for torsion, tensile, and compressive loading, respectively.Figures

Figure 1: Comparison of experimental tension, compression and torsion data with a microstructure-property model. The experiments were performed at a quasi-static strain rate under (a) tension, (b) compression, and (c) torsion loadings with their associated variability.

Figure 2: Comparison of experimental measure material Bauschinger behavior with a microstructure-property model under (a) tension followed by compression, and (b) compression followed by tension with their associated variability.
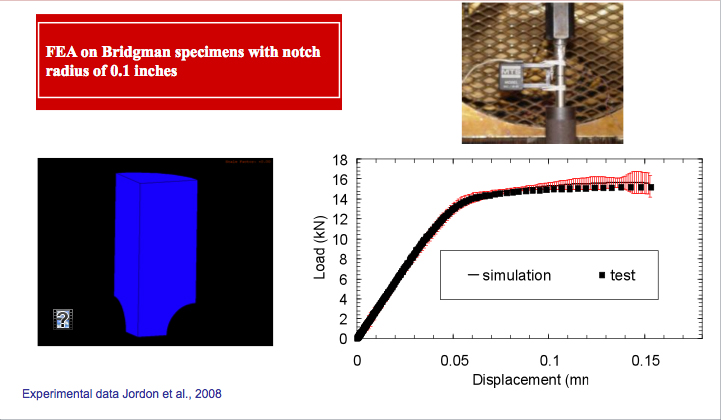
Figure 3: Model validation of FEA simulation using experimental data.
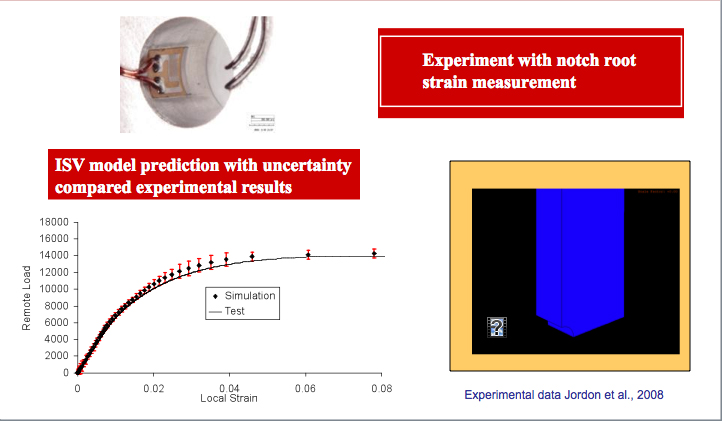
Figure 4: Comparison of experiment to ISV FEA results
