Author(s): Kiran N. Solanki

Overview

Here, we present a methodology for simulation-based product design optimization using an internal state variable (ISV) constitutive modeling approach that captures the microstructure-property relations in the material. By modeling the stochastic uncertainties in the material model and the loading conditions, the design optimization problem is formulated and solved using the reliability-based design optimization (RBDO) methodology. The application problem considers the design optimization of an A356-T6 cast aluminum component under maximum stress and damage constraints. Alternative metamodeling techniques are used to develop appropriate surrogate models in lieu of direct coupling of non-linear static finite element analysis and numerical design optimization. Probabilistic design constraints are modeled using the safety index approach with the solution of the nested optimization problem facilitated with the help of analytical surrogate models. Comparison of the optimization results reveals the importance of using an ISV-based constitutive model that is sensitive to the growth of damage in material. Moreover, the solution of the RBDO problem captures the effects of uncertainty on finding the minimum weight design for the cast component.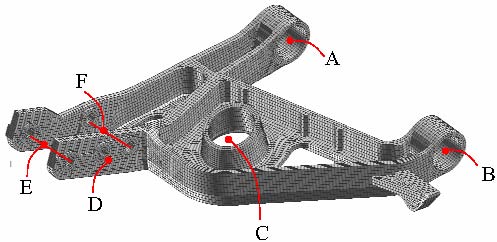

Figure 1: Front Suspension Control Arm FE Model

To illustrate the integration of microstructure-property relations with RBDO methodology, we consider the design of an automobile front suspension control arm as depicted by its FE model in Figure. The control arm is made of A356 aluminum alloy, produced using the die-cast process and then heat treated to T6 condition. This component has been selected because of the availability of data on its load-failure characteristics and the success of microstructure-property relationship model (Horstemeyer and Gokhale, 1999; Horstemeyer et al., 2000; Horstemeyer, 2001) ^[1] in the correct prediction of its failure mode. The two critical loading conditions considered in the design are:

• a 0.8 g panic brake
• b 0.8 g pothole strike.

Both of which are modelled using appropriate boundary conditions (generalized displacements) at the connection points A through F shown in Figure. The FE model is comprised of 22,310 solid elements (C3D8) for 97,440 degrees of freedom. Non-linear static simulations of this high-fidelity model are performed using the FE code, ABAQUS-implicit.

Two different design cases are considered. In the first one, a deterministic optimization problem is set up and solved for minimum weight using two different constitutive models whereas in the second one, an RBDO problem is solved using the uncertainties associated with the loading condition as well as those in the microstructure property relations in the ISV-damage model.

Two different design cases are considered. In the first one, a deterministic optimization problem is set up and solved for minimum weight using two different constitutive models whereas in the second one, an RBDO problem is solved using the uncertainties associated with the loading condition as well as those in the microstructure property relations in the ISV-damage model.

In summary, the steps in formulating and solving the deterministic optimization problem are as follows:

1. Identify the DOE points (design variable values) for both the training and the test design points.
2. Develop a morphed mesh corresponding to each design model in (1) using GENESIS.
3. Perform a non-linear FEA for each design model in (2) using ABAQUS-implicit under the specified loading conditions. Each analysis is performed using:
   1. simple plasticity model (standard ABAQUS material model)
   2. ISV-damage model (DMG 1.0 UMAT)
4. Find the weight as well as the maximum φ and maximum von Mises stress for each design model.
5. Identify the reasonable training points for each material model.
6. Develop six separate metamodels for each response corresponding to (3.1) and (3.2). Evaluate the accuracy of the metamodels and identify the best metamodel for each response.
7. Solve the optimization problem using the selected metamodels.

Conclusions

A methodology for integration of computational material models offering accurate microstructure-property relations with simulation-based design optimization under uncertainty was presented. The successful implementation of the methodology required multiscale material modelling, uncertainty quantification in microstructure-property relations, non-linear static FEA, mesh morphing, development and evaluation of multiple surrogate models, structural reliability analysis for the calculation of safety index and mathematical programming for solution of deterministic and reliability-based optimization problems. The presented methodology provides a means to quantify the trade-off between component geometry and material microstructure. In essence, the methodology allows a designer to optimize the component for strength and/or weight while concurrently developing criteria for tailored microstructures or new materials that will further extend the component capacity. Moreover, the present framework allows a designer to analyze stochastic microstructure distribution effects on the uncertainty of the macroscale mechanical properties. Through the solution of an application problem focusing on the design optimization of an A356-T6 cast aluminum component, two objectives were demonstrated:

1. the advantage of using an ISV-damage model over the standard plasticity model for accurate prediction of damage.
2. the quantification of stochastic uncertainties at the microstructure level and their propagation to macroscopic responses for use in reliability-based design optimization.

Based on the solution of the application problem, the following conclusions can be drawn:

• When using the damage/failure criterion, the design variables had a highly non-linear and noisy effect.
• Not all metamodels can accurately capture a noisy and non-linear response, especially when the design and random variables combined are used as input variables.
• Mesh morphing was effective in altering the component geometry and sizing of a new structural component.
• Due to its smaller damage level, the optimum design based on ISV-damage constitutive model was found to be superior to that based on simple plasticity models for the same weight.
• Although a safety factor of two for load resulted in a safety factor of approximately two for stresses, it led to a much greater safety factor in terms of damage. Hence, the load safety factor must be selected with caution.
• In comparison to the baseline model, the control arm design optimization resulted in a weight saving of approximately 25% while increasing component safety by an order of magnitude. One could effectively save more weight if the damage levels were designed to be similar.

Resources

1. ↑ Solanki, K.N., Acar, E., Rais-Rohani, M., Horstemeyer, M., & Steele, G. (Oct 2009). Product Design Optimization with Microstructure-Property Modeling and Associated Uncertainties. International Journal of Design Engineering Inderscience Publishers, 2(1), 47-79.
   (http://www.inderscience.com/search/index.php?action=record&rec_id=28446)