A constitutive model for amorphous thermoplastics using a thermodynamic approach with physically motivated internal state variables has been developed to predict the complex mechanical behavior of polymers. The formulation follows current internal state variable methodologies used for metals and departs from the spring-dashpot representation generally used to characterize the mechanical behavior of polymers. The selection of internal state variables was guided by a hierarchical multiscale modeling approach that bridged deformation mechanisms from the molecular dynamics scale (coarse grain model) to the continuum level. The model equations were developed within a large deformation kinematics and thermodynamics framework where the hardening behavior at large strains was captured using a kinematic-type hardening variable with two possible evolution laws: a current method based on hyperelasticity theory and an alternate method whereby kinematic hardening depends on chain stretching and material plastic flow. The three dimensional equations were then reduced to the one-dimensional case to quantify the material parameters from monotonic compression test data at different applied strain rates. To illustrate the generalized nature of the constitutive model, material parameters were determined for four different amorphous polymers: polycarbonate, poly(methylmethacrylate), polystyrene, and poly(2,6-dimethyl-1,4-phenylene oxide). This model captures the complex character of the stress-strain behavior of these amorphous polymers for a range of strain rates.^[1]

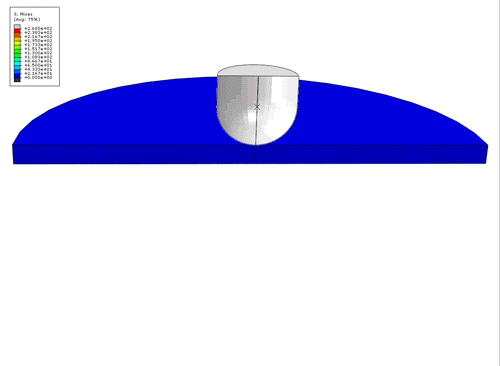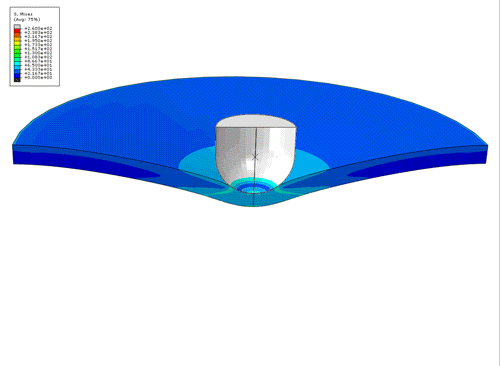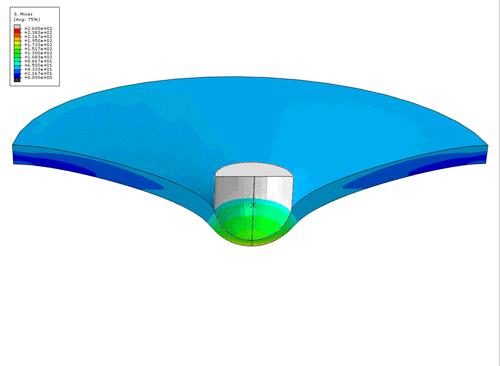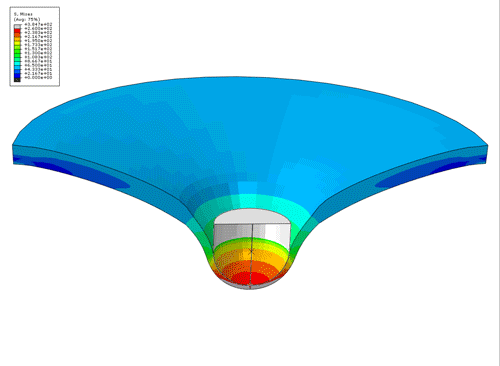
SHPB FE animation of the Von Mises Stress contours for a SHPB test. Upper movie insert is actual experiment and lower animation is FE simulation of test, at 550 s^-1.