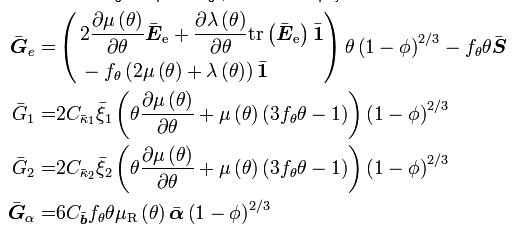Abstract

The following article proposes a damage model that is implemented into a glassy, amorphous thermoplastic thermomechanical inelastic internal state variable framework. Internal state variable evolution equations are defined through thermodynamics, kinematics, and kinetics for isotropic damage arising from two different inclusion types: pores and particles. The damage arising from the particles and crazing is accounted for by three processes of damage: nucleation, growth, and coalescence. Nucleation is defined as the number density of voids/crazes with an associated internal state variable rate equation and is a function of stress state, molecular weight, fracture toughness, particle size, particle volume fraction, temperature, and strain rate. The damage growth is based upon a single void growing as an internal state variable rate equation that is a function of stress state, rate sensitivity, and strain rate. The coalescence internal state variable rate equation is an interactive term between voids and crazes and is a function of the nearest neighbor distance of voids/crazes and size of voids/crazes, temperature, and strain rate. The damage arising from the pre-existing voids employs the Cocks–Ashby void growth rule. The total damage progression is a summation of the damage volume fraction arising from particles and pores and subsequent crazing. The modeling results compare well to experimental findings garnered from the literature. Finally, this formulation can be readily implemented into a finite element analysis.

Constitutive Model

sition of the deformation gradient (deviatoric plasic, voluemtric plastic/damage, thermal, and elastic):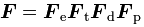

Cauchy Stress:

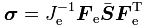
Second Piola-Kirchhoff Stress (intermediate state):

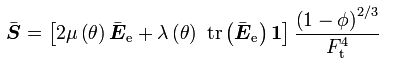
Shear and bulk moduli: (Lamé parameters)

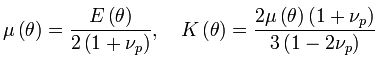
Temperature dependent Young's Modulus:

Assuming isotropic damage, the three stress-like thermodynamic conjugates to the ISVs become:

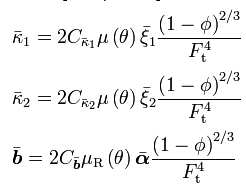
The evolution of ISV (entanglement density):

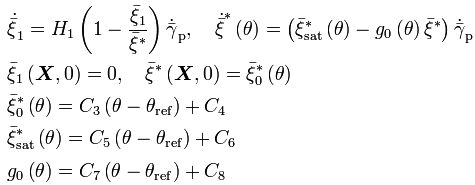
The evolution of ISV (large-strain chain alignment/coiling):

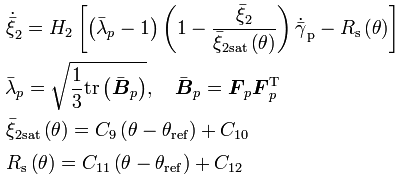
Viscous shear strain rate:

The evolution of ISV (large-strain chain hardening due to chain stretch):

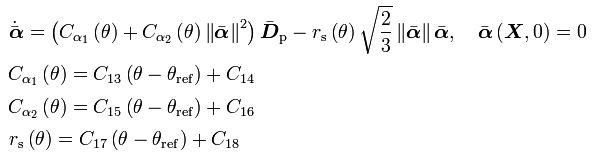
Plastic flow rule

Total damage evolution

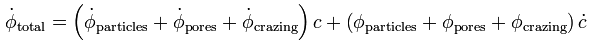
Particle damage evolution

Particle damage nucleation evolution

Particle growth around a void

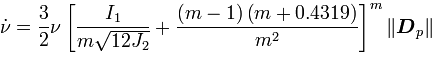
Pore growth evolution

Crazing evolution

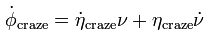
Craze nucleation

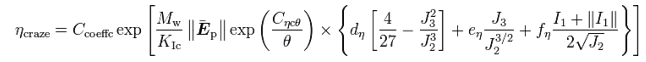
Coalescence

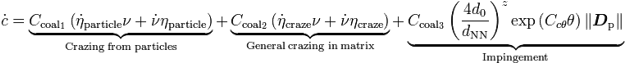
Temperature Evolution

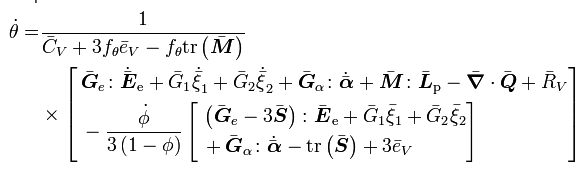
and when assuming isotropic damage, the G terms simplify to

Publication

D.K. Francis, J.L. Bouvard, Y. Hammi, M.F. Horstemeyer, Formulation of a damage internal state variable model for amorphous glassy polymers, International Journal of Solids and Structures, Vol 51, Issues 15–16, Pages 2765–2776, 2014.